Points On The Unit Circle
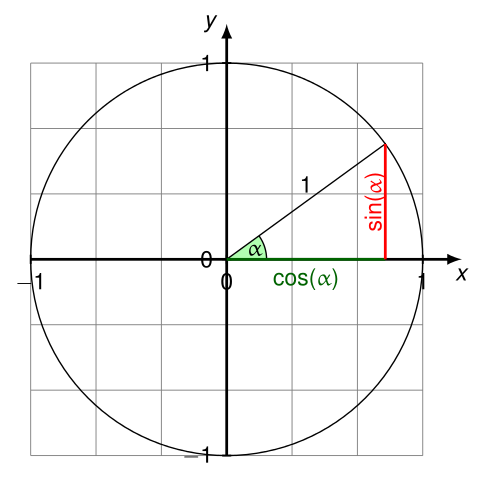
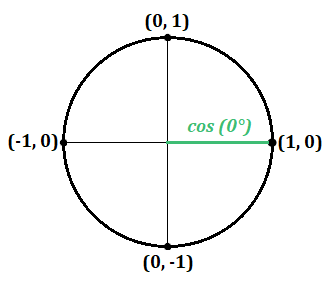
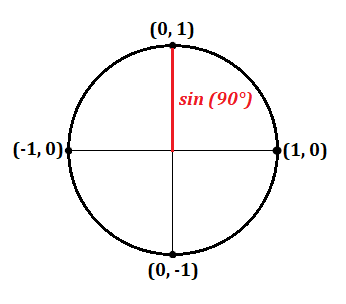
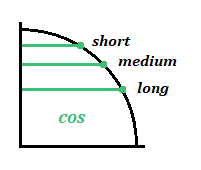
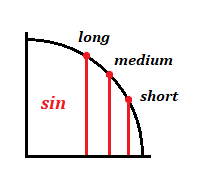
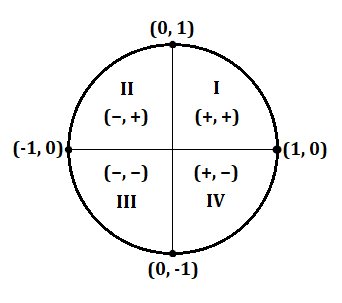
If you lot're studying trig or calculus—or getting ready to—you'll demand to get familiar with the unit of measurement circle. The unit of measurement circle isan essential tool used to solve for the sine, cosine, and tangent of an angle. Just how does it work? And what information do you demand to know in order to use it? In this article, we explicate what the unit of measurement circle is and why you should know it. We also requite you three tips to help yous remember how to employ the unit of measurement circle. Feature Prototype: Gustavb/Wikimedia The unit circle is a circle with a radius of 1. This ways that for any straight line drawn from the center point of the circle to whatsoever point forth the edge of the circle, the length of that line will ever equal 1. (This also ways that the diameter of the circumvolve will equal 2, since the bore is equal to twice the length of the radius.) Typically, the eye betoken of the unit of measurement circle is where the x-centrality and y-axis intersect, or at the coordinates (0, 0): The unit of measurement circumvolve, or trig circle every bit it's too known, is useful to know because information technology lets us easily calculate the cosine, sine, and tangent of any angle between 0° and 360° (or 0 and 2π radians). Every bit you can see in the to a higher place diagram, by drawing a radius at whatever bending (marked past ∝ in the image), you volition be creating a right triangle. On this triangle, the cosine is the horizontal line, and the sine is the vertical line. In other words,cosine = x-coordinate, and sine = y-coordinate. ( The triangle'south longest line, or hypotenuse, is the radius and therefore equals ane.) Why is all of this of import? Remember that you lot can solve for the lengths of the sides of a triangle using the Pythagorean theorem, or $a^2+b^ii=c^2$ (in which a and b are the lengths of the sides of the triangle, and c is the length of the hypotenuse). We know that the cosine of an bending is equal to the length of the horizontal line, the sine is equal to the length of the vertical line, and the hypotenuse is equal to 1. Therefore, we tin can say that the formula for whatever right triangle in the unit of measurement circumvolve is as follows: $$\cos^2θ+\sin^2θ=1^2$$ Since $1^ii=i$, we can simplify this equation like this: $$\cos^2θ+\sin^2θ=i$$ Be aware thatthese values tin can exist negative depending on the angle formed and what quadrant the ten- and y-coordinates fall in (I'll explicate this in more than detail later). Here is an overview of all major angles in degrees and radians on the unit circle: Simply what if at that place's no triangle formed? Let's expect at what happens when the angle is 0°, creating a horizontal direct line along the x-centrality: On this line, the x-coordinate equals ane and the y-coordinate equals 0. We know that the cosine is equal to the x-coordinate, and the sine is equal to the y-coordinate, so we tin write this: What if the angle is ninety° and makes a perfectly vertical line along the y-axis? Here, we tin can see that the x-coordinate equals 0 and the y-coordinate equals 1. This gives usa the following values for sine and cosine: As stated above, the unit circle is helpful because it allows us to easily solve for the sine, cosine, or tangent of any caste or radian. It's especially useful to know the unit circle nautical chart if you need to solve for certain trig values for math homework or if you're preparing to study calculus. Just how exactly tin can knowing the unit circle help you? Let'south say you're given the following trouble on a math test—and are non allowed to use a calculator to solve information technology: $$\sin30°$$ Where practise you starting time? Allow'south take a look at the unit circle chart again—this time with all major angles (in both degrees and radians) and their corresponding coordinates: Don't get overwhelmed! Remember, all you're solving for is $\sin30°$. Past looking at this chart, we tin can see that the y-coordinate is equal to $1/ii$ at thirty°. And since the y-coordinate equals sine, our respond is every bit follows: $$\sin30°=ane/2$$ Only what if you get a problem that uses radians instead of degrees? The procedure for solving it is nonetheless the same. Say, for example, you get a trouble that looks like this: $$\cos{{3π}/four}$$ Again, using the chart above, we can see that the x-coordinate (or cosine) for ${3π}/4$ (which is equal to 135°) is $-{√ii}/ii$. Here's what our answer to this problem would look like then: $$\cos({3π}/four)=-{√2}/2$$ All of this is pretty easy if you accept the unit circle chart above to use equally a reference. Only well-nigh (if not all) of the time, this won't be the case, and you lot'll be expected to respond these types of math questions using your encephalon only. So how can you lot remember the unit circle? Read on for our summit tips! In this section, we requite you our acme tips for remembering the trig circle so you tin apply information technology with ease for any math trouble that requires it. In club to employ the unit circle effectively, y'all'll need to memorize the most common angles (in both degrees and radians) as well every bit their corresponding x- and y-coordinates. The diagram to a higher place is a helpful unit circle chart to look at, since it includes all major angles in both degrees and radians, in addition to their respective coordinate points along the ten- and y-axes. Here is a chart listing this same data in table class: Angle (Degrees) Angle (Radians) Coordinates of Point on Circle 0° / 360° 0 / 2π (1, 0) 30° $π/6$ $({√3}/2, 1/2)$ 45° $π/iv$ $({√2}/2, {√2}/ii)$ sixty° $π/iii$ $(1/2,{√3}/2)$ ninety° $π/2$ (0, 1) 120° ${2π}/3$ $(-1/2, {√three}/two)$ 135° ${3π}/iv$ $(-{√ii}/2, {√two}/two)$ 150° ${5π}/6$ $(-{√three}/ii, i/ii)$ 180° π (-1, 0) 210° ${7}/6$ $(-{√three}/two, -1/2)$ 225° ${5π}/4$ $(-{√2}/2, -{√ii}/ii)$ 240° ${4π}/3$ $(-1/2, -{√3}/two)$ 270° ${3π}/2$ (0, -1) 300° ${5π}/three$ $(1/2, -{√3}/2)$ 315° ${7π}/4$ $({√two}/two, -{√ii}/2)$ 330° ${11π}/6$ $({√3}/two, -ane/2)$ Now, while y'all're more welcome to effort to memorize all these coordinates and angles, this is a lot of stuff to remember. Fortunately, at that place's a trick you tin can utilize to help you remember the most important parts of the unit circumvolve. Expect at the coordinates above and y'all'll find a clear pattern: all points (excluding those at 0°, 90°, 270°, and 360°) alternate between just 3 values (whether positive or negative): Each value corresponds to a short, medium, or long line for both cosine and sine: Hither's what these lengths mean: For example, if yous're trying to solve $\cos{π/three}$, you should know correct away that this bending (which is equal to threescore°) indicates a short horizontal line on the unit of measurement circle. Therefore,its corresponding x-coordinate must equal $1/2$ (a positive value, since $π/three$ creates a indicate in the first quadrant of the coordinate organization). Finally, while information technology's helpful to memorize all the angles in the table higher up, note that past far the nearly important angles to think are the following: It's disquisitional to exist able to distinguish positive and negative ten- and y-coordinates so that you're finding the correct value for a trig problem. As a reminder,west hether a coordinate on the unit of measurement circle will be positive or negative depends on which quadrant (I, II, III, or Four) the indicate falls under: Here's a chart showing whether a coordinate volition be positive or negative based on the quadrant a detail bending (in degrees or radians) is in: Quadrant X-Coordinate (Cosine) Y-Coordinate (Sine) I + + II − + III − − IV + − For example, say you're given the following problem on a math exam: $$\cos210°$$ Before you fifty-fifty try to solve it, y'all should be able to recognize that the reply volition be a negative number since the angle 210° falls in quadrant III (where x-coordinates are always negative). Now, using the play tricks we learned in tip 1, you can figure out that an angle of 210° creates a long horizontal line. Therefore, our answer is as follows: $$\cos210°=-{√3}/2$$ Lastly, information technology's essential to know how to use all of this information about the trig circle and sine and cosine in order to be able to solve for the tangent of an angle. In trig, to find the tangent of an angle θ (in either degrees or radians), y'all simply divide the sine by the cosine: $$\tanθ={\sinθ}/{\cosθ}$$ For instance, say you're trying to answer this problem: $$\tan300°$$ The kickoff stride is to set up an equation in terms of sine and cosine: $$\tan300°={\sin300°}/{\cos300°}$$ Now, to solve for the tangent, we need to notice the sine and cosine of 300°. You should exist able to quickly recognize that the angle 300° falls in the fourth quadrant, pregnant that the cosine, or x-coordinate, volition be positive, and the sine, or y-coordinate, will be negative. You should likewise know right away that the angle 300° creates a short horizontal line and a long vertical line. Therefore, the cosine (the horizontal line) volition equal $one/2$, and the sine (the vertical line) will equal $-{√iii}/ii$ (a negative y-value, since this point is in quadrant IV). Now, to find the tangent, all you practice is plug in and solve: $$\tan300°={-{√iii}/2}/{1/2}$$ $$\tan300°=-√3$$ Now that you know what the unit of measurement circle looks similar and how to use it, permit'south test what you've learned with a few practice problems. With this problem, at that place are two pieces of information you should exist able to place right away: Since 45° indicates a positive, medium-length line, the correct answer is ${√2}/2$. If you lot're not sure how to effigy this out, draw a diagram to aid you make up one's mind whether the length of the line will be short, medium, or long. Similar problem #i above, there are two pieces of information you lot should be able to quickly grasp with this problem: Since 240° indicates a negative, short line, the right answer is $-i/two$. Unlike the bug to a higher place, this problem uses radians instead of degrees. Although this might brand the problem look trickier to solve, in reality it uses the same bones steps as the other 2 problems. Outset, you lot should recognize that the angle ${5π}/3$ is in quadrant IV, and then the x-coordinate, or cosine, will be a positive number. You should likewise be able to tell that ${5π}/iii$ creates a curt horizontal line. This gives you enough information to determine that theanswer is $1/2$. This problem deals with tangent instead of sine or cosine, which means that it'll require a trivial more than math on our end. Offset off, call up the bones formula for finding tangent: $$\tan θ={\sin θ}/{\cos θ}$$ Now, let's have the caste we've been given—${2π}/3$—and plug information technology into this equation: $$\tan {2π}/3={\sin {2π}/three}/{\cos {2π}/iii}$$ Yous should at present exist able to solve for the sine and cosine separately using what you lot've memorized nigh the unit circumvolve. Since the angle ${2π}/iii$ is in quadrant II, the 10-coordinate (or cosine) will be negative, and the y-coordinate (or sine) volition be positive. Next, yous should exist able to determine based on the angle alone that the horizontal line is a short line, and the vertical line is a long line. This means that the cosine is equal to $-1/two$, and the sine is equal to ${√iii}/2$. At present that we've figured out these values, all nosotros have to do is plug them into our initial equation and solve for the tangent: $$\tan {2π}/iii={{√3}/2}/{-1/2}$$ $$\tan {2π}/3=-√3$$ If you're taking the SAT or Deed soon, you lot'll need to know some trig so you can practice well on the math section. Take a look at our expert guides to trig on the SAT and ACT so you tin acquire exactly what you'll need to know for test day! Besides memorizing the unit of measurement circle, it's a adept idea to learn how to plug in numbers and how to plug in answers. Read our guides to acquire all about these two useful strategies, which you tin can use on whatsoever math test—including the Sat and Human activity!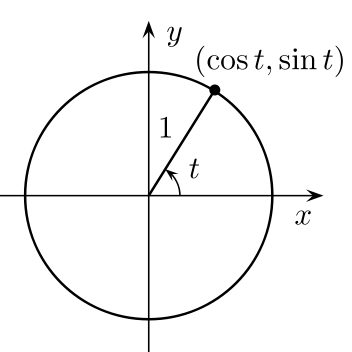
The Unit Circle: A Basic Introduction
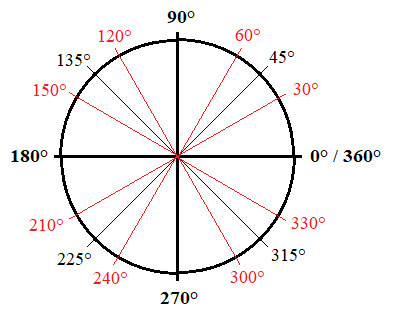
Unit Circle — Degrees
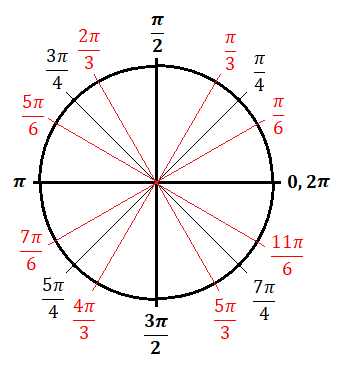
Unit Circumvolve — Radians
 This slogan definitely applies if y'all're not a math lover.
This slogan definitely applies if y'all're not a math lover. Why Yous Should Know the Unit Circle
 Jim.belk/Wikimedia
Jim.belk/Wikimedia How to Recall the Unit Circle: 3 Essential Tips
 I wouldn't recommend practicing the unit circumvolve with postal service-its, but, hey, information technology'due south a start.
I wouldn't recommend practicing the unit circumvolve with postal service-its, but, hey, information technology'due south a start. #1: Memorize Mutual Angles and Coordinates
 Treat your negatives and positives as you would cables that can potentially kill you if hooked upwardly incorrectly.
Treat your negatives and positives as you would cables that can potentially kill you if hooked upwardly incorrectly. #2: Learn What's Negative and What's Positive
#3: Know How to Solve for Tangent
 Fourth dimension to purr-actice your math skills!
Fourth dimension to purr-actice your math skills! Unit of measurement Circle Practice Question Prepare
Questions
Answers
Answer Explanations
#one: $\sin45°$
#2: $\cos240°$
#3: $\cos{5π}/3$
#4: $\tan{2π}/3$
What'southward Next?

About the Author
Hannah received her MA in Japanese Studies from the University of Michigan and holds a available's caste from the Academy of Southern California. From 2013 to 2015, she taught English in Japan via the JET Plan. She is passionate about education, writing, and travel.
Points On The Unit Circle,
Source: https://blog.prepscholar.com/unit-circle-chart-radians-degrees
Posted by: albrittonoughted2001.blogspot.com


0 Response to "Points On The Unit Circle"
Post a Comment